e-mail: taohou at uoregon dot edu
Announcement
- I am looking for PhD students to work with me (Fall25' still open!). Send me an email if you are interested; see also the 'To Perspective Students' section for details.
About
I am an Assistant Professor in the CS department at the University of Oregon. My research interest is computational topology/geometry and topological data analysis (TDA). I am also broadly interested in applications of TDA to different domains.
I graduated from the CS department at Purdue University with a doctoral degree, advised by Dr. Tamal K. Dey. I spent the first four years of my PhD at The Ohio State University (and later on transferred to Purdue with my advisor). The title of my PhD thesis is 'Homological Representatives in Topological Persistence'. Before doing my PhD, I received an M.E. degree in Software Engineering from Tsinghua University and a B.E. degree in Software Engineering from Beijing Institute of Technology, both in China.
To Perspective Students
The core of my research is a combination of computer science with mathematics, and I am open to working with students who have a strong interest in either, or both. Students with CS or Math background are welcomed to contact me. Meanwhile, I am also broadly interested in applications of my research to different domains. I am seeking more extensive interplay of TDA with areas such as machine learning, geometry processing, visualizations, etc. (To know more, see this presentation I gave, a course I teach on my research field, and a nice tutorial on topological machine learning.)
As a student of mine, you will pursue a research effort in any one or combination of the following directions:
- Applications (machine learning, analyzing domain data, etc.)
- Efficient algorithm design and computational complexity
- Applied mathematics (topology, geometry, algebra, etc.)
Software
Publications
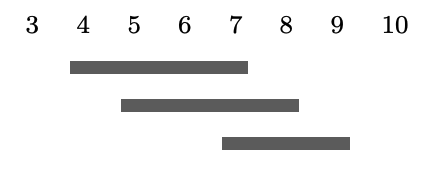
Tao Hou*, Salman Parsa*, and Bei Wang*
International Symposium on Computational Geometry (SoCG) 2025
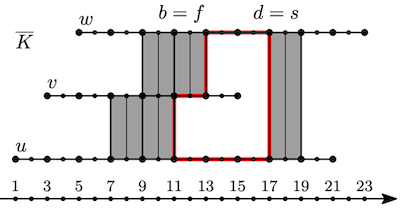
Tamal K. Dey*, Tao Hou*, and Dmitriy Morozov*
International Symposium on Computational Geometry (SoCG) 2025
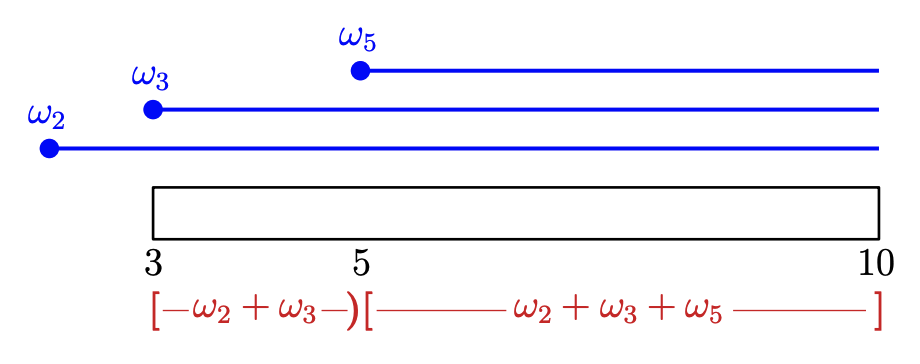
Tamal K. Dey*, Tao Hou*, and Dmitriy Morozov*
ACM-SIAM Symposium on Discrete Algorithms (SODA) 2025
[talk@SODA]
Nghi Nguyen, Tao Hou, Enrico Amico, Jingyi Zheng, Huajun Huang, Alan D. Kaplan, Giovanni Petri, Joaquin Goni, Yize Zhao, Duy Duong-Tran, and Li Shen
International Conference on Medical Image Computing and Computer Assisted Intervention (MICCAI) 2024
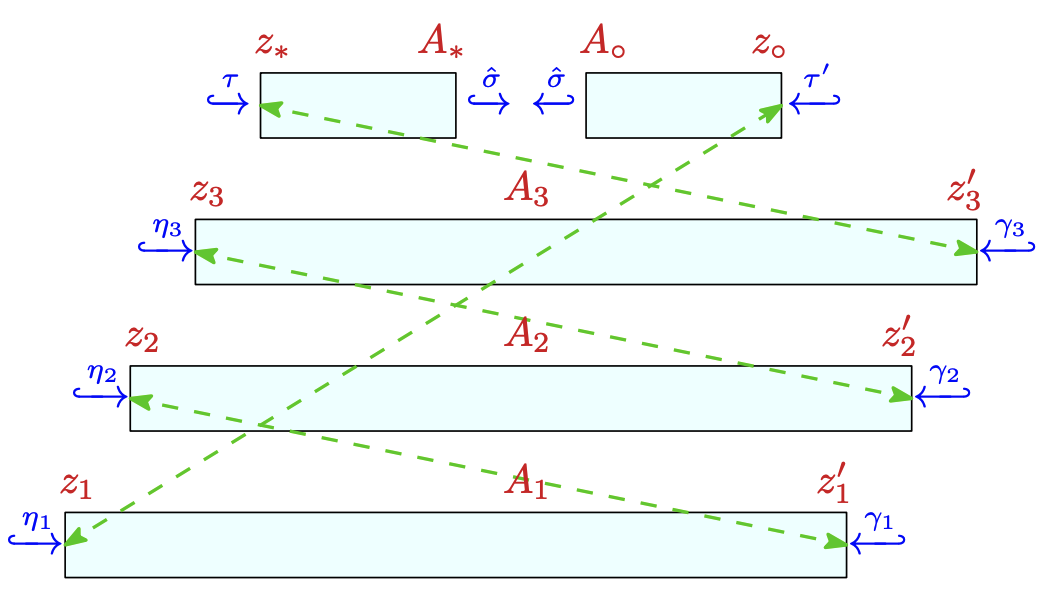
Tamal K. Dey* and Tao Hou*
International Symposium on Computational Geometry (SoCG) 2024
Tamal K. Dey*, Tao Hou*, and Salman Parsa*
Algorithms and Data Structures Symposium (WADS) 2023,
[talk@WADS]
Tamal K. Dey* and Tao Hou*
arXiv preprint arXiv: 2112.02352 (2022)
[github]
Tamal K. Dey* and Tao Hou*
European Symposium on Algorithms (ESA) 2022
[github] [talk@ESA]
On Association between Absolute and Relative Zigzag Persistence
Tamal K. Dey*, Tao Hou*, and Anirudh Pulavarthy*
arXiv preprint arXiv:2105.00518 (2021)
[github]
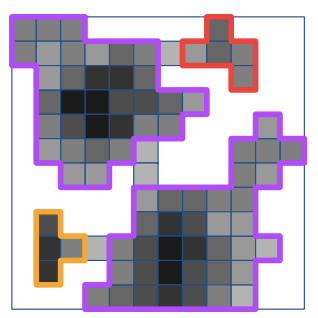
Anand V. Patel, Tao Hou, Juan D. Beltran Rodriguez, Tamal K. Dey, and Dunbar P. Birnie III
Computational Materials Science, 202:110920, 2022
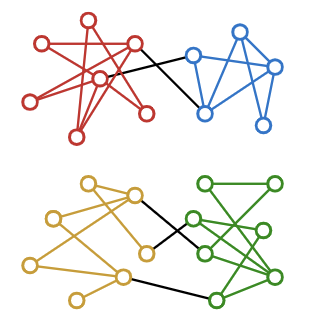
Tamal K. Dey* and Tao Hou*
International Symposium on Computational Geometry (SoCG) 2021
[talk@SoCG]
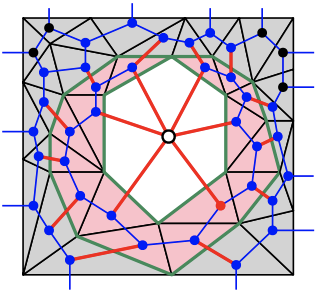
Tamal K. Dey*, Tao Hou*, and Sayan Mandal*
ACM-SIAM Symposium on Discrete Algorithms (SODA) 2020
[github] [talk@SODA]
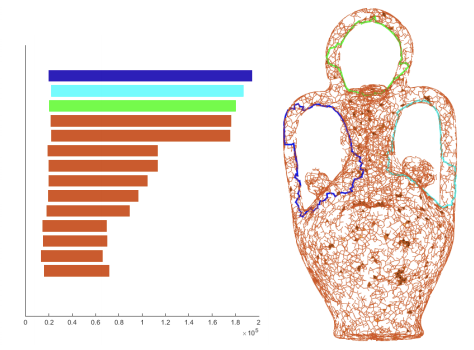
Tamal K. Dey*, Tao Hou*, and Sayan Mandal*
Computational Topology in Image Context, International Workshop, 2019
[webpage] [talk@Ohio TDA Day]
Tao Hou and Li Chen
Journal of Visualization 19.4 (2016): 715-726
Miscellaneous
- A talk I gave at the Oregon State Geometry and Topology Seminars on several of my works for computing zigzag persistence
- A lecture I gave on the Gudhi library
Invited Talks / Conference Presentations
A Fast Algorithm for Computing Zigzag Representatives SODA. Jan 2025. New Orleans, Louisiana
Can zigzag persistence be computed as efficiently as the standard version?
Geometry/Topology Seminars, Oregon State Univ.
Oct 2024. Corvallis, OR
Can zigzag persistence be computed as efficiently as the standard version?
Computational Persistence Workshop 2024 (online).
Sep 2024. TU Graz, Austria
Revisiting Graph Persistence for Updates and Efficiency WADS. Jul 2023. Montreal, QC
Revisiting computation of zigzag persistence for new results TDA Seminar, Michigan State Univ. Dec 2022. East Lansing, MI
Fast Computation of Zigzag Persistence Computational Persistence Workshop. Nov 2022. Purdue University (online)
Fast Computation of Zigzag Persistence ESA. Sep 2022. Potsdam, Germany (online)
Topological Signatures for Data Analysis Aided by Homological Generators Seminar, North Carolina State University. Mar 2022. Raleigh, NC
Computing zigzag persistence on graphs in near-linear time Computational Persistence Workshop. Nov 2021. Purdue University (online)
Computing zigzag persistence on graphs in near-linear time SoCG. Jun 2021. Buffalo, New York (online)
Computing minimal persistent cycles: polynomial and hard cases Seminar, Topology and Geometry for Data Analysis, Purdue University. Feb 2021. Online
Computing minimal persistent cycles: polynomial and hard cases Seminar, Applied Algebraic Topology Research Network. May 2020. Online
Computing minimal persistent cycles: polynomial and hard cases SODA. Jan 2020. Salt Lake City, Utah
Persistent 1-cycles: definition, computation, and some applications Ohio TDA Day. July 2019. Dayton, Ohio
Teaching
CS 410/510: Topological Methods in Data Analysis and Machine Learning
CS 621: Algorithms and Complexity